31 下一个排列

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1
“下一个排列”的定义是：给定数字序列的字典序中下一个更大的排列。如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

我们可以将该问题形式化地描述为：给定若干个数字，将其组合为一个整数。如何将这些数字重新排列，以得到下一个更大的整数。如 123 下一个更大的数为 132。如果没有更大的整数，则输出最小的整数。

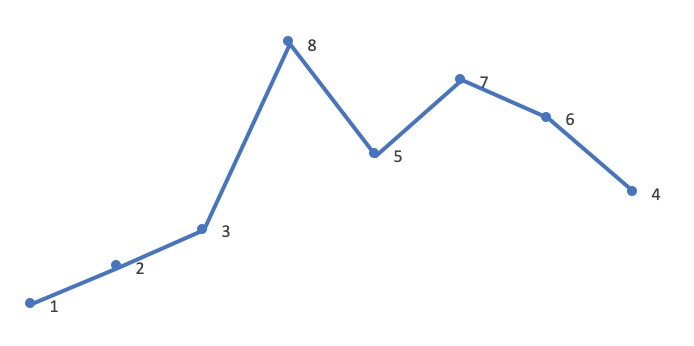
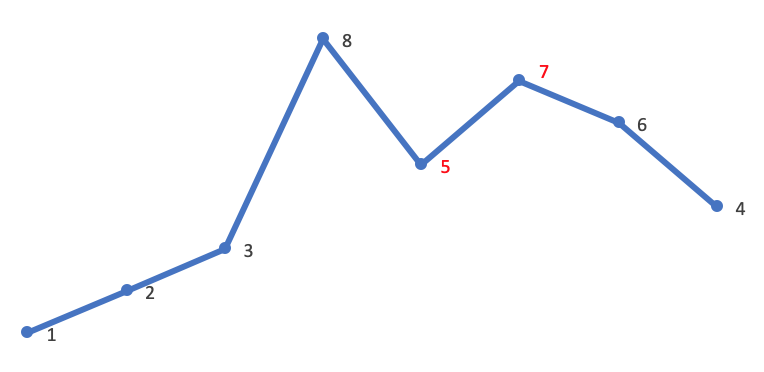
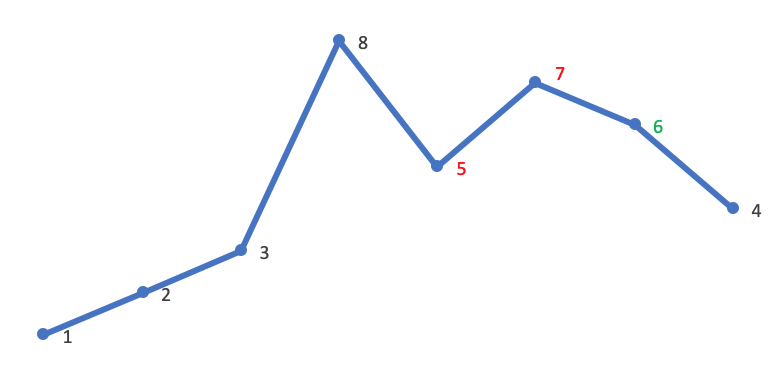
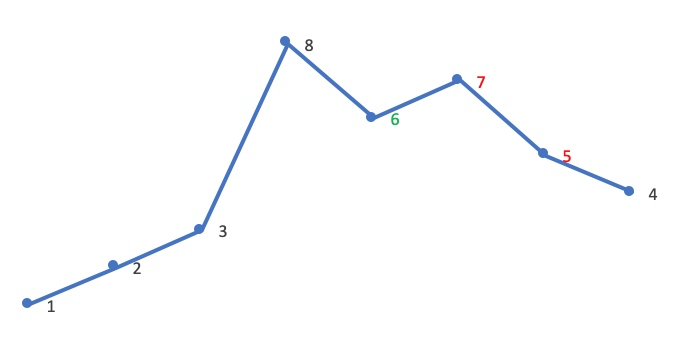
以 1,2,3,4,5,6 为例，其排列依次为：
123456
123465
123546
...
654321

1
2
3
4
5
6
7
8

如何得到这样的排列顺序？这是本文的重点。我们可以这样来分析：

1.我们希望下一个数比当前数大，这样才满足“下一个排列”的定义。因此只需要将后面的「大数」与前面的「小数」交换，就能得到一个更大的数。比如 123456，将 5 和 6 交换就能得到一个更大的数 123465。
2.我们还希望下一个数增加的幅度尽可能的小，这样才满足“下一个排列与当前排列紧邻“的要求。为了满足这个要求，我们需要：
（1）在尽可能靠右的低位进行交换，需要从后向前查找
（2）将一个 尽可能小的「大数」 与前面的「小数」交换。比如 123465，下一个排列应该把 5 和 4 交换而不是把 6 和 4 交换
（3）将「大数」换到前面后，需要将「大数」后面的所有数重置为升序，升序排列就是最小的排列。以 123465 为例：首先按照上一步，交换 5 和 4，得到 123564；然后需要将 5 之后的数重置为升序，得到 123546。显然 123546 比 123564 更小，123546 就是 123465 的下一个排列
以上就是求“下一个排列”的分析过程。

1
2
3
4
5
6
7

标准的“下一个排列”算法可以描述为：

1.从后向前查找第一个**==相邻升序==**的元素对 (i,j)，满足 A[i] < A[j]。此时 [j,end) 必然是降序
2.在 [j,end) 从后向前查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
3.将 A[i] 与 A[k] 交换
4.可以断定这时 [j,end) 必然是降序，逆置 [j,end)，使其升序
5.如果在步骤 1 找不到符合的相邻元素对，说明当前 [begin,end) 为一个降序顺序，则直接跳到步骤 4

1

以求 12385764 的下一个排列为例：

1

首先从后向前查找第一个相邻升序的元素对 (i,j)。这里 i=4，j=5，对应的值为 5，7：

1

然后在 [j,end) 从后向前查找第一个大于 A[i] 的值 A[k]。这里 A[i] 是 5，故 A[k] 是 6：

1

将 A[i] 与 A[k] 交换。这里交换 5、6：

1

这时 [j,end) 必然是降序，逆置 [j,end)，使其升序。这里逆置 [7,5,4]：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

因此，12385764 的下一个排列就是 12386457。

最后再可视化地对比一下这两个相邻的排列（橙色是蓝色的下一个排列）：
class Solution:
    def nextPermutation(self, nums) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        length = len(nums)
        guard = -1
        guard_index = length + 1
        index = length - 1
        while (index - 1) >= 0:
            if nums[index - 1] < nums[index]:
                guard = nums[index - 1]
                guard_index = index - 1
                break
            index = index - 1

        # print("guard_index = {}, guard = {}".format(guard_index, guard))
        if guard_index == (length + 1):
            return nums.sort(reverse=False)

        cur_index = length - 1
        while cur_index > guard_index:
            if nums[cur_index] > guard:
                break
            cur_index -= 1

        if cur_index >= length:
            cur_index = index
        nums[cur_index], nums[guard_index] = nums[guard_index], nums[cur_index]

        for i in range(guard_index + 1, length - 1):
            for j in range(guard_index + 1, length - 1):
                if nums[j] > nums[j + 1]:
                    nums[j], nums[j + 1] = nums[j + 1], nums[j]