17 电话号码的字母组合

1
2
3

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

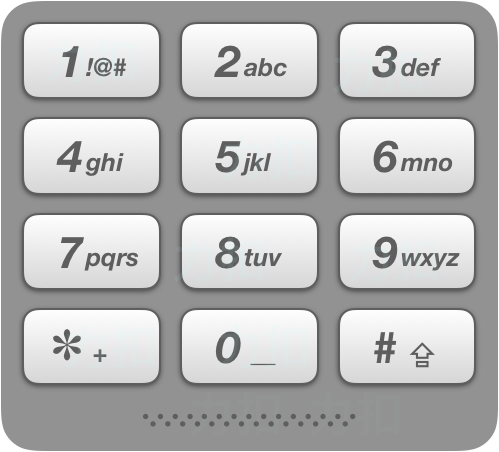
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
方法：回溯
回溯是一种通过穷举所有可能情况来找到所有解的算法。如果一个候选解最后被发现并不是可行解，回溯算法会舍弃它，并在前面的一些步骤做出一些修改，并重新尝试找到可行解。

给出如下回溯函数 backtrack(combination, next_digits) ，它将一个目前已经产生的组合 combination 和接下来准备要输入的数字 next_digits 作为参数。

如果没有更多的数字需要被输入，那意味着当前的组合已经产生好了。
如果还有数字需要被输入：
遍历下一个数字所对应的所有映射的字母。
将当前的字母添加到组合最后，也就是 combination = combination + letter 。
重复这个过程，输入剩下的数字： backtrack(combination + letter, next_digits[1:]) 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Solution:
    def letterCombinations(self, digits: str):
        if len(digits) == 0:
            return []
        number_al_dict = {
            '2': 'abc',
            '3': 'def',
            '4': 'ghi',
            '5': 'jkl',
            '6': 'mno',
            '7': 'pqrs',
            '8': 'tuv',
            '9': 'wxyz'
        }
        if len(digits) == 1:
            return [i for i in number_al_dict[digits[0]]]

        tmp = []
        output = []

        def backtrack(path, next_numbers):
            if len(next_numbers) == 0:
                tmp.append(path)
                output.append("".join(path))
                return

            for letter in number_al_dict[next_numbers[0]]:
                # if letter in path:
                #     continue
                path.append(letter)
                backtrack(path, next_numbers[1:])
                path.pop()

        backtrack([], digits)
        return output