https://blog.csdn.net/liuwei0604/article/details/50414542 马拉车算法可以在线性时间复杂度内求出一个字符串的最长回文字串。其核心思想跟 KMP 相似,即反复利用已掌握的情况。
1.整体思路
1
2
3
|
这个算法的主要思路是维护一个跟原串 str 一样长的数组 lens。lens[i] 表示以 str[i] 为中点的回串其中一边的长度。这里有的人把中点算进去,有的人记录两边的长度,其实都一样,我这里是只记录一边的长度,不包括中点。比如 "CDCDE"
str: [C, D, C, D, E]
lens: [0, 1, 1, 0, 0]
|
那么 lens 里最大的自然就对应最长回串的中点了。所以这个算法的核心就是如何快速计算 lens。
2.预处理
1
2
3
4
5
6
7
8
9
10
11
12
13
|
回文有奇偶长度两种情况,通过补充间隔符可以将这两种情况化简为奇数长度。
比如 ABA 补充为 #A#B#A# 中点还是 B,ABBA 补充为 #A#B#B#A# 中点为 #,最后可以去掉。
算法用 JavaScript 写,我将原串转为数组,间隔符就用 null。
最后在两侧补上哨兵点方便遍历中止。我用了 NaN。所以看起来是这样
var arr = [NaN, null]
for (let i = 0; i < str.length; i += 1) {
arr.push(str[i])
arr.push(null)
}
arr.push(NaN)
|
3.详解
1
2
3
4
5
6
|
马拉车算法 Manacher‘s Algorithm 是用来查找一个字符串的最长回文子串的线性方法,由一个叫 Manacher 的人在 1975 年发明的,这个方法的最大贡献是在于将时间复杂度提升到了线性。
首先我们解决下奇数和偶数的问题,在每个字符间插入 "#",并且为了使得扩展的过程中,到边界后自动结束,在两端分别插入 "^" 和 "$",两个不可能在字符串中出现的字符,这样中心扩展的时候,判断两端字符是否相等的时候,如果到了边界就一定会不相等,从而出了循环。经过处理,字符串的长度永远都是奇数了。
马拉车算法 Manacher‘s Algorithm 是用来查找一个字符串的最长回文子串的线性方法,由一个叫 Manacher 的人在 1975 年发明的,这个方法的最大贡献是在于将时间复杂度提升到了线性。
首先我们解决下奇数和偶数的问题,在每个字符间插入 "#",并且为了使得扩展的过程中,到边界后自动结束,在两端分别插入 "^" 和 "$",两个不可能在字符串中出现的字符,这样中心扩展的时候,判断两端字符是否相等的时候,如果到了边界就一定会不相等,从而出了循环。经过处理,字符串的长度永远都是奇数了。
|

1
|
首先我们用一个数组 P 保存从中心扩展的最大个数,而它刚好也是去掉 "#" 的原字符串的总长度。例如下图中下标是 6 的地方,可以看到 P[ 6 ] 等于 5,所以它是从左边扩展 5 个字符,相应的右边也是扩展 5 个字符,也就是 "#c#b#c#b#c#"。而去掉 # 恢复到原来的字符串,变成 "cbcbc",它的长度刚好也就是 5。
|

4.求原字符串下标
1
2
3
|
用 P 的下标 i 减去 P [ i ],再除以 2,就是原字符串的开头下标了。
例如我们找到 P[ i ] 的最大值为 5,也就是回文串的最大长度是 5,对应的下标是 6,所以原字符串的开头下标是(6 - 5 )/ 2 = 0。所以我们只需要返回原字符串的第 0 到 第(5 - 1)位就可以了。
|
5.求每个 P [ i ]
1
2
3
4
5
6
7
|
接下来是算法的关键了,它充分利用了回文串的对称性。
我们用 C 表示回文串的中心,用 R 表示回文串的右边半径。所以 R = C + P[ i ]。C 和 R 所对应的回文串是当前循环中 R 最靠右的回文串。
让我们考虑求 P [ i ] 的时候,如下图。
用 i_mirror 表示当前需要求的第 i 个字符关于 C 对应的下标。
|

1
2
3
|
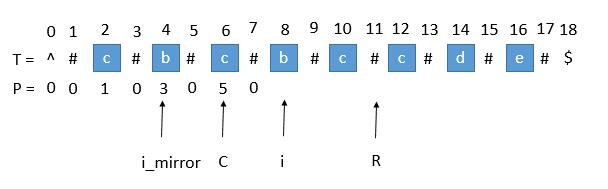
我们现在要求 P [ i ],如果是用中心扩展法,那就向两边扩展比对就行了。但是我们其实可以利用回文串 C 的对称性。i 关于 C 的对称点是 i_mirror,P [ i_mirror ] = 3,所以 P [ i ] 也等于 3。
但是有三种情况将会造成直接赋值为 P [ i_mirror ] 是不正确的,下边一一讨论。
|
(1)超出了R

1
|
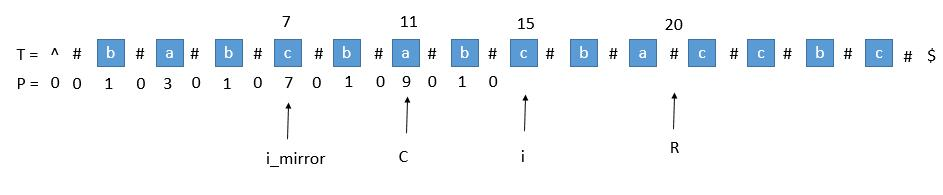
当我们要求 P [ i ] 的时候,P [ mirror ] = 7,而此时 P [ i ] 并不等于 7,为什么呢,因为我们从 i 开始往后数 7 个,等于 22,已经超过了最右的 R,此时不能利用对称性了,但我们一定可以扩展到 R 的,所以 P [ i ] 至少等于 R - i = 20 - 15 = 5,会不会更大呢,我们只需要比较 T [ R+1 ] 和 T [ R+1 ]关于 i 的对称点就行了,就像中心扩展法一样一个个扩展。
|
(2) P [ i_mirror ] 遇到了原字符串的左边界
1
|
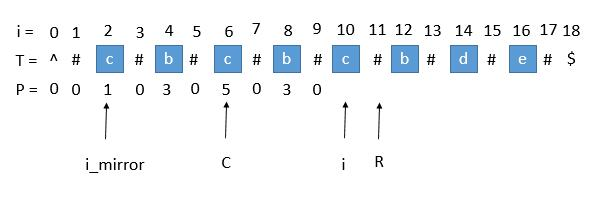
此时P [ i_mirror ] = 1,但是 P [ i ] 赋值成 1 是不正确的,出现这种情况的原因是 P [ i_mirror ] 在扩展的时候首先是 "#" == "#",之后遇到了 "^" 和另一个字符比较,也就是到了边界,才终止循环的。而 P [ i ] 并没有遇到边界,所以我们可以继续通过中心扩展法一步一步向两边扩展就行了。
|
(3)i 等于了 R
1
|
此时我们先把 P [ i ] 赋值为 0,然后通过中心扩展法一步一步扩展就行了。
|
6.考虑 C 和 R 的更新
1
|
就这样一步一步的求出每个 P [ i ],当求出的 P [ i ] 的右边界大于当前的 R 时,我们就需要更新 C 和 R 为当前的回文串了。因为我们必须保证 i 在 R 里面,所以一旦有更右边的 R 就要更新 R。
|

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
|
此时的 P [ i ] 求出来将会是 3,P [ i ] 对应的右边界将是 10 + 3 = 13,所以大于当前的 R,我们需要把 C 更新成 i 的值,也就是 10,R 更新成 13。继续下边的循环。
public String preProcess(String s) {
int n = s.length();
if (n == 0) {
return "^$";
}
String ret = "^";
for (int i = 0; i < n; i++)
ret += "#" + s.charAt(i);
ret += "#$";
return ret;
}
// 马拉车算法
public String longestPalindrome2(String s) {
String T = preProcess(s);
int n = T.length();
int[] P = new int[n];
int C = 0, R = 0;
for (int i = 1; i < n - 1; i++) {
int i_mirror = 2 * C - i;
if (R > i) {
P[i] = Math.min(R - i, P[i_mirror]);// 防止超出 R
} else {
P[i] = 0;// 等于 R 的情况
}
// 碰到之前讲的三种情况时候,需要利用中心扩展法
while (T.charAt(i + 1 + P[i]) == T.charAt(i - 1 - P[i])) {
P[i]++;
}
// 判断是否需要更新 R
if (i + P[i] > R) {
C = i;
R = i + P[i];
}
}
// 找出 P 的最大值
int maxLen = 0;
int centerIndex = 0;
for (int i = 1; i < n - 1; i++) {
if (P[i] > maxLen) {
maxLen = P[i];
centerIndex = i;
}
}
int start = (centerIndex - maxLen) / 2; //最开始讲的求原字符串下标
return s.substring(start, start + maxLen);
}
class Solution:
def longestPalindrome(self, s):
format_s = self.pre_process(s)
length = len(format_s)
ps = [0] * length
center = 0
right = 0
for current in range(1, length - 1):
current_mirror = 2 * center - current
if (current + ps[current_mirror]) < right and (current_mirror - 1) != 0:
ps[current] = ps[current_mirror]
elif (current + ps[current_mirror]) < right and (current_mirror - 1) == 0:
i = 1
while (current - i) >= 0 and (current + i) < length and format_s[current - i] == format_s[current + i]:
ps[current] += 1
i+=1
if ps[current] < ps[current_mirror]:
ps[current] = ps[current_mirror]
else:
i = 1
while (current - i) >= 0 and (current + i) < length and format_s[current - i] == format_s[
current + i]:
ps[current] += 1
i += 1
if ps[current] + center > right:
center = current
right = ps[current] + center
max_length = 0
center_index = 0
for i in range(1, length -1):
if ps[i] > max_length:
max_length = ps[i]
center_index = i
start = (center_index - max_length) // 2
return s[start:start + max_length]
def pre_process(self, s):
result = "#"
for i in range(len(s)):
result += s[i]
result += '#'
return result
if __name__ == '__main__':
solution = Solution()
result = solution.longestPalindrome("ababcbab")
print(result)
时间复杂度:for 循环里边套了一层 while 循环,难道不是 O(n²)?不!其实是 O(n)。不严谨的想一下,因为 while 循环访问 R 右边的数字用来扩展,也就是那些还未求出的节点,然后不断扩展,而期间访问的节点下次就不会再进入 while 了,可以利用对称得到自己的解,所以每个节点访问都是常数次,所以是 O ( n )。
空间复杂度:O(n)。
|
总结
1
2
3
4
5
6
|
时间复杂度从三次方降到了一次,美妙!这里两次用到了动态规划去求解,初步认识了动态规划,就是将之前求的值保存起来,方便后边的计算,使得一些多余的计算消失了。并且在动态规划中,通过观察数组的利用情况,从而降低了空间复杂度。而 Manacher 算法对回文串对称性的充分利用,不得不让人叹服,自己加油啦
作者:windliang
链接:https://leetcode-cn.com/problems/longest-palindromic-substring/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-bao-gu/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
|